Introducción
Estuve leyendo un artículo sobre como graficar los “paralelogramos de primos” en J usando verbos (en ingés), que está basado en la segunda parte de un video de Numberphile (en ingés).La idea es tomar el n-ésimo primo y restarle el número que se obtiene invirtiendo el orden de su representación en base 2. Por ejemplo, el 16-avo primo es 53=1101012, al darlo vuelta queda 1010112=43, así que el valor es 53-43=10. Al graficar esta función aparecen unos paralelogramos.
La duda que me surgió es qué pasaba si graficábamos todos los números en vez de dibujar sólo los primos. Y además entender de dónde vienen estos paralelogramos.
Módulos adicionales
Para graficarlos en Racket vamos a necesitar usar algunos modulos adicionales, así que empezamos con#lang racket
(require math/number-theory)
(require plot)
#;(plot-new-window? #t)
A mí también me gusta modificar cómo aparecen los números en los ejes. Es medio técnico y casi o cambia el resultado. El código está abajo.
Reconstruyendo el dibujo
Primero definimos la función que invierte el orden de los bits en la representación binaria del número.(define (binary-reverse x)
(let loop ([x x] [r 0])
(if (zero? x)
r
(loop (quotient x 2) (+ (* 2 r) (remainder x 2))))))
Veamos algunos ejemplos
(for ([i (in-range 16)])
(define r (binary-reverse i))
(displayln (list i r (number->string i 2) (number->string r 2))))
> (0 0 0 0)
> (1 1 1 1)
> (2 1 10 1)
> (3 3 11 11)
> (4 1 100 1)
> (5 5 101 101)
> (6 3 110 11)
> (7 7 111 111)
> (8 1 1000 1)
> (9 9 1001 1001)
> (10 5 1010 101)
> (11 13 1011 1101)
> (12 3 1100 11)
> (13 11 1101 1011)
> (14 7 1110 111)
> (15 15 1111 1111)
Nota: Es posible definirla usando strings, pero usar strings siempre es mucho más lento que operar directamente con los números enteros.
Para simplificar la notación, llamemos inv a esta función que invierte el orden de los bits, p a la función que calcula el n-esimo primo y f a f(n)=n-inv(n).
Ahora podemos hacernos una lista con los puntos (n, f(p(n))) = (n, p(n) - inv(p(n))) en forma de vectores.
(define prim/original (for/list ([i (in-naturals 1)]
[p (in-list (next-primes 1 10000))])
(vector i (- p (binary-reverse p)))))
Nota: Es posible escribir nuestra propia función para tertear primalidad, pero las funciones next-primes y prime? son mejores.
Y la dibujamos con plot
(plot (points prim/original))
Arreglamos el color y la opacidad para que el dibujo sea más lindo
(plot #:title "Prime Paralelograms (original)"
(points prim/original
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "n" #:y-label "f(p(n))"
#:x-min 0)
Para guardar la imagen usamos plot-file
(plot-file #:title "Prime Paralelograms (original)"
(points prim/original
#:sym 'dot
#:color 'blue #:alpha .5)
"prime-paralelograms(original).png"
#:x-label "n" #:y-label "f(p(n))"
#:x-min 0)
Para poder compararla con el próximo gráfico, la dibujamos de vuelta. Pero con las etiquetas de los valores del eje x hacia la izquierda (para que el borde del gráfico sea el borde de la imagen).
(parameterize ([plot-x-tick-label-anchor 'top-right])
(plot #:title "Prime Paralelograms (original)"
(points prim/original
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "n" #:y-label "f(p(n))"
#:x-min 0))
Ahora cambiamos lo que graficamos. Cambiamos la posición en x de los puntos, en vez de tomar el número de primo tomamos el valor del primo, o sea que en vez de dibujar (n, f(p(n)) dibujamos (p(n), f(p(n)) = (p, f(p)).
(define prim/new (for/list ([i (in-naturals 1)]
[p (in-list (next-primes 1 10000))])
(vector p (- p (binary-reverse p)))))
(parameterize ([plot-x-tick-label-anchor 'top-right])
(plot #:title "Prime Paralelograms"
(points prim/new
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "p(n)" #:y-label "f(p(n))"
#:x-min 0))
Podemos compararlo con el dibujo anterior:
El dibujo que obtenemos es muy similar, si ignoramos la escala del eje x. Los paralelogramos cortan en posiciones ligeramente diferentes, pero son muy parecidos.
Lo que pasa es que si dibujamos el n-esimo primo obtenemos casi una recta.
(define prim/scale (for/list ([i (in-naturals 1)]
[p (in-list (next-primes 1 10000))])
(vector i p)))
(plot #:title "Primes"
(points prim/scale
#:sym 'dot)
#:x-label "n" #:y-label "p(n) = nth prime"
#:x-min 0)
La inversa es la función que cuenta la cantidad de primos que en general se llama pi(n) y su pendiente va cambiando lentamente, más o menos como 1/log(n), pero log(n) es una función que crece muy lentamente. Así que el cambio entre los gráficos es casi una transformación lineal y por eso a cambiar el eje en los dibujos anteriores vemos que la forma de los paralelogramos cambia poco. (Deberíamos poder notar más distorsión en los primeros paralelogramos.)
Comparando con todos los números
Veamos ahora como queda el gráfico cuando usamos todos los números en vez de sólo los primos. Para poder comparar mejor los gráficos, fijamos el mismo rango para el eje y en todos los gráficos. Además, me gusta elegir un tamaño de gráfico para que la recta y=x tenga aproximadamente 45°. (En Excel uno hace un gráfico y después con el mouse arregla todos los detalles de los ejes y escalas. Acá hay que poner todo eso en el programa para que las escalas queden exactamente como uno quiere.)(define all (for/list ([i (in-range 1 131072)])
(vector i (- i (binary-reverse i)))))
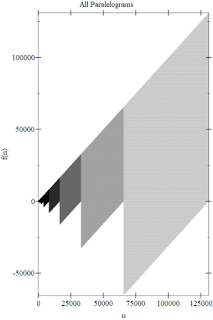
(plot #:title "All Paralelograms"
(points all
#:sym 'dot
#:color 'black #:alpha .1)
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
Repetimos el gráfico de los primos en la misma escala, armando la lista de primos en este rango de una manera ligeramente diferente.
(define prim (for/list ([i (in-range 1 131072)]
#:when (prime? i))
(vector i (- i (binary-reverse i)))))
(plot #:title "Prime Paralelograms"
(points prim
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "p" #:y-label "f(p)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
Y los superponemos
(plot #:title "All vs Prime Paralelograms"
(list (points all
#:sym 'dot
#:color 'black #:alpha .1)
(points prim
#:sym 'dot
#:color 'blue #:alpha .5))
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
[Gráfico]
Lo que vemos es que los paralelogramos de los primos ocupan la mitad de abajo de los paralelogramos que se forman cuando graficamos todos los números.
Pares e impares
Casi todos los primos son impares. Por ser impares al invertir el orden de sus cifras en binario se obtiene un número con la misma cantidad de cifras en binario. Así que es aproximadamente del mismo tamaño. Se pueden hacer algunas acotaciones y formalizar esta idea, pero es más lindo comparar en el gráfico que pasa cuando reemplazamos los números primos por los números impares.(define odd (for/list ([i (in-range 1 131072 2)])
(vector i (- i (binary-reverse i)))))
(plot #:title "All vs Odd Paralelograms"
(list (points all
#:sym 'dot
#:color 'black #:alpha .1)
(points odd
#:sym 'dot
#:color 'red #:alpha .1))
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
Vemos que los impares ocupan el esencialmente los mismos paralelogramos, aunque hay menos huecos.
En cambio, los números pares terminan en 0 en binario, así que al invertir el orden de sus cifras en binario al menos pierden una cifra y son más chicos. Al dibujar tenemos
(define even (for/list ([i (in-range 2 131072 2)])
(vector i (- i (binary-reverse i)))))
(plot #:title "All vs Even Paralelograms"
(list (points all
#:sym 'dot
#:color 'black #:alpha .1)
(points even
#:sym 'dot
#:color 'green #:alpha .1))
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
Vemos que los pares ocupan esencialmente las mitades de arriba, o sea que no se superponen con lo pintado por los primos. Entonces que los huequitos en los paralelogramos de los primos se deben a números impares no primos.
Algunas ideas para probar
- ¿Qué pasa en base 3? ¿Es la generalización obvia? ¿En base 4 son banderitas?
- Redibujar para ver sólo los primeros paralelogramos. El cambio de escala no es tan lineal al principio y al dibujar los paralelogramos del artículo original (n, f(p(n)) deberían estar más deformados.
- Redibujar todo con el eje x en escala logarítmica para que todos los paralelogramos tengan el mismo ancho y se pueda ver bien los primeros. No sé qué escala usar para el eje y. ¿Quizás haya que dibujar cada paralelogramo por separado?
- Los primos no son aleatorios, pero parecen bastante aleatorios. Podría ser interesante generar una lista de truchi-primos, filtrando los números impares con una distribución parecida a la de los primos y ver cómo queda el gráfico.
Cambiando el formato de las etiquetas
A mí me gusta modificar cómo aparecen los números en los ejes, no me gusta que 100000 aparece como 105. Esta parte es medio técnica y casi no cambia el resultado, así que no voy a explicar los detalles. (Parece una buena idea para un PR como una opción adicional de linear-ticks.)(require plot/utils)
(define ((linear-ticks-format/no-sc) min max pre-ticks)
(define digits (digits-for-range min max))
(map (lambda (pt)
(real->plot-label (pre-tick-value pt) digits #f))
pre-ticks))
(define (linear-ticks/no-sc) (ticks (linear-ticks-layout) (linear-ticks-format/no-sc)))
(plot-x-ticks (linear-ticks/no-sc)) ; almost global change
(plot-y-ticks (linear-ticks/no-sc)) ; almost global change
Código completo
#lang racket(require math/number-theory)
(require plot)
#;(plot-new-window? #t)
(require plot/utils)
(define ((linear-ticks-format/no-sc) min max pre-ticks)
(define digits (digits-for-range min max))
(map (lambda (pt)
(real->plot-label (pre-tick-value pt) digits #f))
pre-ticks))
(define (linear-ticks/no-sc) (ticks (linear-ticks-layout) (linear-ticks-format/no-sc)))
(plot-x-ticks (linear-ticks/no-sc)) ; almost global change
(plot-y-ticks (linear-ticks/no-sc)) ; almost global change
(define (binary-reverse x)
(let loop ([x x] [r 0])
(if (zero? x)
r
(loop (quotient x 2) (+ (* 2 r) (remainder x 2))))))
(for ([i (in-range 16)])
(define r (binary-reverse i))
(displayln (list i r (number->string i 2) (number->string r 2))))
#;(for ([i (in-range 128)]
#:when (prime? i))
(define r (binary-reverse i))
(displayln (list i r (number->string i 2) (number->string r 2))))
;ORIGINAL
(define prim/original (for/list ([i (in-naturals 1)]
[p (in-list (next-primes 1 10000))])
(vector i (- p (binary-reverse p)))))
(plot (points prim/original))
(plot #:title "Prime Paralelograms (original)"
(points prim/original
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "n" #:y-label "f(p(n))"
#:x-min 0)
(plot-file #:title "Prime Paralelograms (original)"
(points prim/original
#:sym 'dot
#:color 'blue #:alpha .5)
"prime-paralelograms(original).png"
#:x-label "n" #:y-label "f(p(n))"
#:x-min 0)
(parameterize ([plot-x-tick-label-anchor 'top-right])
(plot #:title "Prime Paralelograms (original)"
(points prim/original
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "n" #:y-label "f(p(n))"
#:x-min 0))
;NEW
(define prim/new (for/list ([i (in-naturals 1)]
[p (in-list (next-primes 1 10000))])
(vector p (- p (binary-reverse p)))))
(parameterize ([plot-x-tick-label-anchor 'top-right])
(plot #:title "Prime Paralelograms"
(points prim/new
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "p(n)" #:y-label "f(p(n))"
#:x-min 0))
;SCALE
(define prim/scale (for/list ([i (in-naturals 1)]
[p (in-list (next-primes 1 10000))])
(vector i p)))
(plot #:title "Primes"
(points prim/scale
#:sym 'dot)
#:x-label "n" #:y-label "p(n) = nth prime"
#:x-min 0)
;All
(define all (for/list ([i (in-range 1 131072)])
(vector i (- i (binary-reverse i)))))
(plot #:title "All Paralelograms"
(points all
#:sym 'dot
#:color 'black #:alpha .1)
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
(define prim (for/list ([i (in-range 1 131072)]
#:when (prime? i))
(vector i (- i (binary-reverse i)))))
(plot #:title "Prime Paralelograms"
(points prim
#:sym 'dot
#:color 'blue #:alpha .5)
#:x-label "p" #:y-label "f(p)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
(plot #:title "All vs Prime Paralelograms"
(list (points all
#:sym 'dot
#:color 'black #:alpha .1)
(points prim
#:sym 'dot
#:color 'blue #:alpha .5))
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
; ODD and EVEN
(define odd (for/list ([i (in-range 1 131072 2)])
(vector i (- i (binary-reverse i)))))
(plot #:title "All vs Odd Paralelograms"
(list (points all
#:sym 'dot
#:color 'black #:alpha .1)
(points odd
#:sym 'dot
#:color 'red #:alpha .1))
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)
(define even (for/list ([i (in-range 2 131072 2)])
(vector i (- i (binary-reverse i)))))
(plot #:title "All vs Even Paralelograms"
(list (points all
#:sym 'dot
#:color 'black #:alpha .1)
(points even
#:sym 'dot
#:color 'green #:alpha .1))
#:x-label "n" #:y-label "f(n)"
#:y-min -65536 #:y-max 131072
#:x-min 0
#:width 400 #:height 600)